Forever丶CIL 首页文章列表标签分类
多边形分割成若干凸多边形（NavMesh的初步形成）
|游戏开发

多边形分割成若干凸多边形（NavMesh的初步形成）

本文基于 Arkin, Ronald C.的论文 “Path planning for a vision-based autonomous robot”.
论文链接 Path planning for a vision-based autonomous robot
部分计算几何的算法基于Computational Geometry in C
其源码可以参考：orourke-compc

现任佐治亚理工教授 Ronald C. Arkin，在1986年时发表了一篇叫做Path planning for a vison-based autonomous robot的报告，隶属robotics领域。文章提出了Meadow Map的方法以长时间存储地图。Meadow Map为现代Navmesh系统的雏形，提出了以下核心观点：

  • 使用凸多边形构建可行走区域

  • 对生成的凸多边形集合，以其公共边中点为寻路节点，使用A*进行寻路

  • 使用路径改进算法，对A*结果进行改良

在本文中，我们主要探讨：通过Arkin教授的方法去实现给定一个任意多边形，得到其分割而成的若干凸多边形。

方法步骤：

  1. 对于现有的多边形$P$，若其为凸多边形，则结束，否则进入步骤2

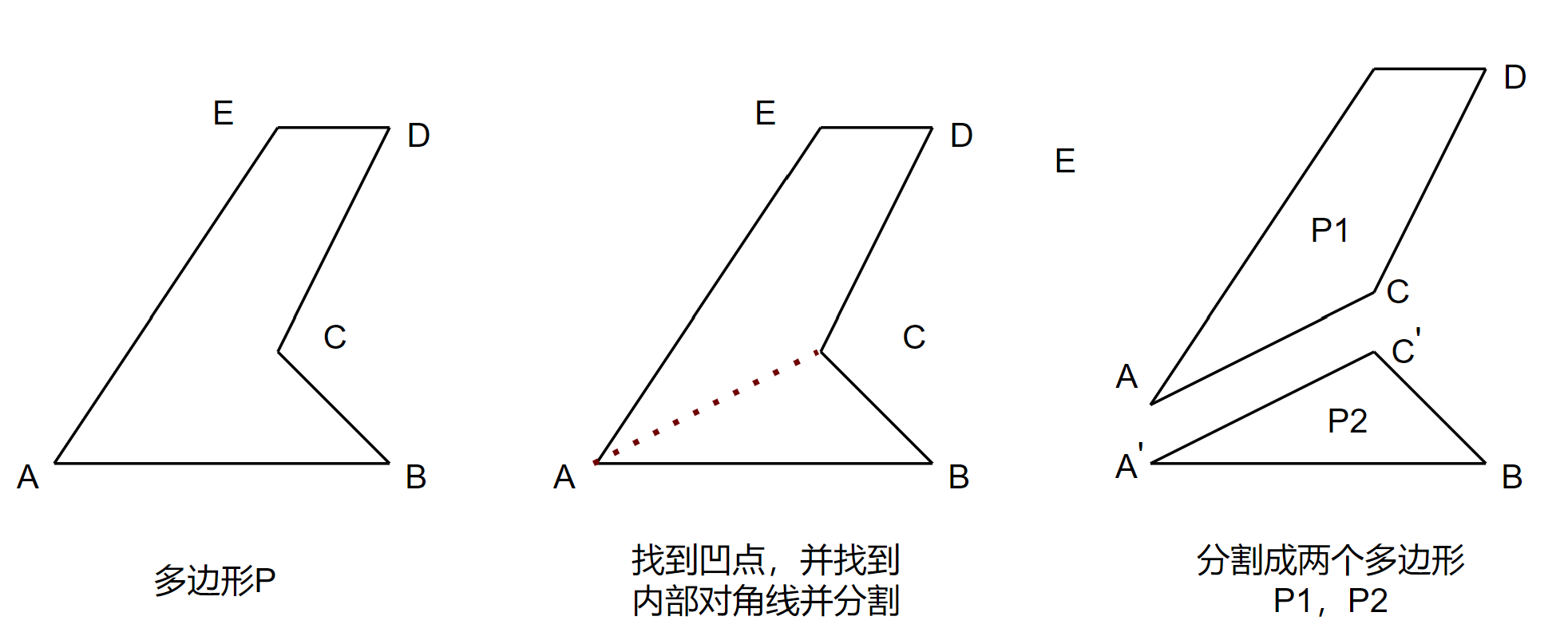
  2. 在$P$中找到一个凹的点，如图中点$A$

  3. 由点$A$去找一个同在$P$中的另一不相邻点，如图中$D, E, H$等

  4. 选择其中一个完全在$P$内部的线段，用于将$P$分割成两个子多边形$P_1, P_2$

  5. 对$P_1, P_2$做同样的操作

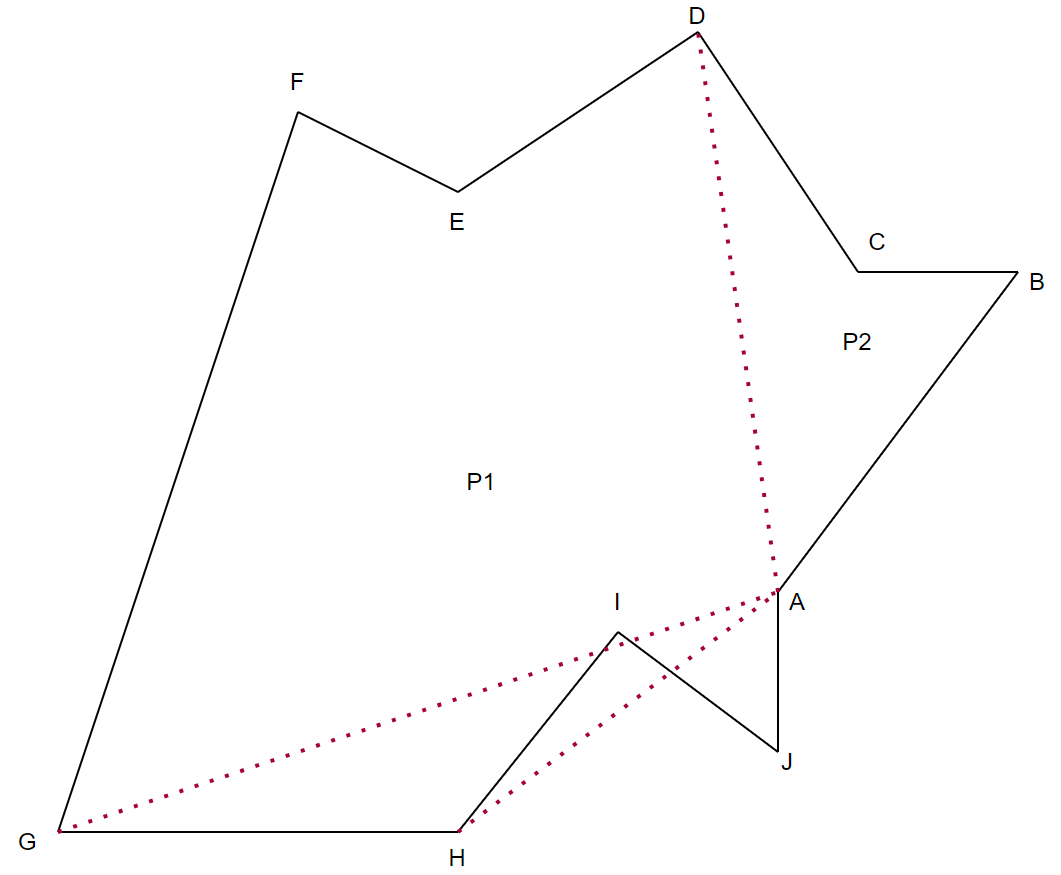
线段是否完全在多边形内部

完全在$P$内部（例如图中线段$AD$）的判断方式：

  • 在角的内侧（对于$AD$来说就是要在$∠JAB$和$∠CDE$的内侧）

  • 不与任何一条非相邻边相交（对于$AD$来说就是不与$AJ, AB, DC, DE$以外的边相交）

在上图中，线段$AG, AH$都是反例，要被排除掉，我们可以在$AC, AD, AE, AF$中选择一条去分割多边形$P$。

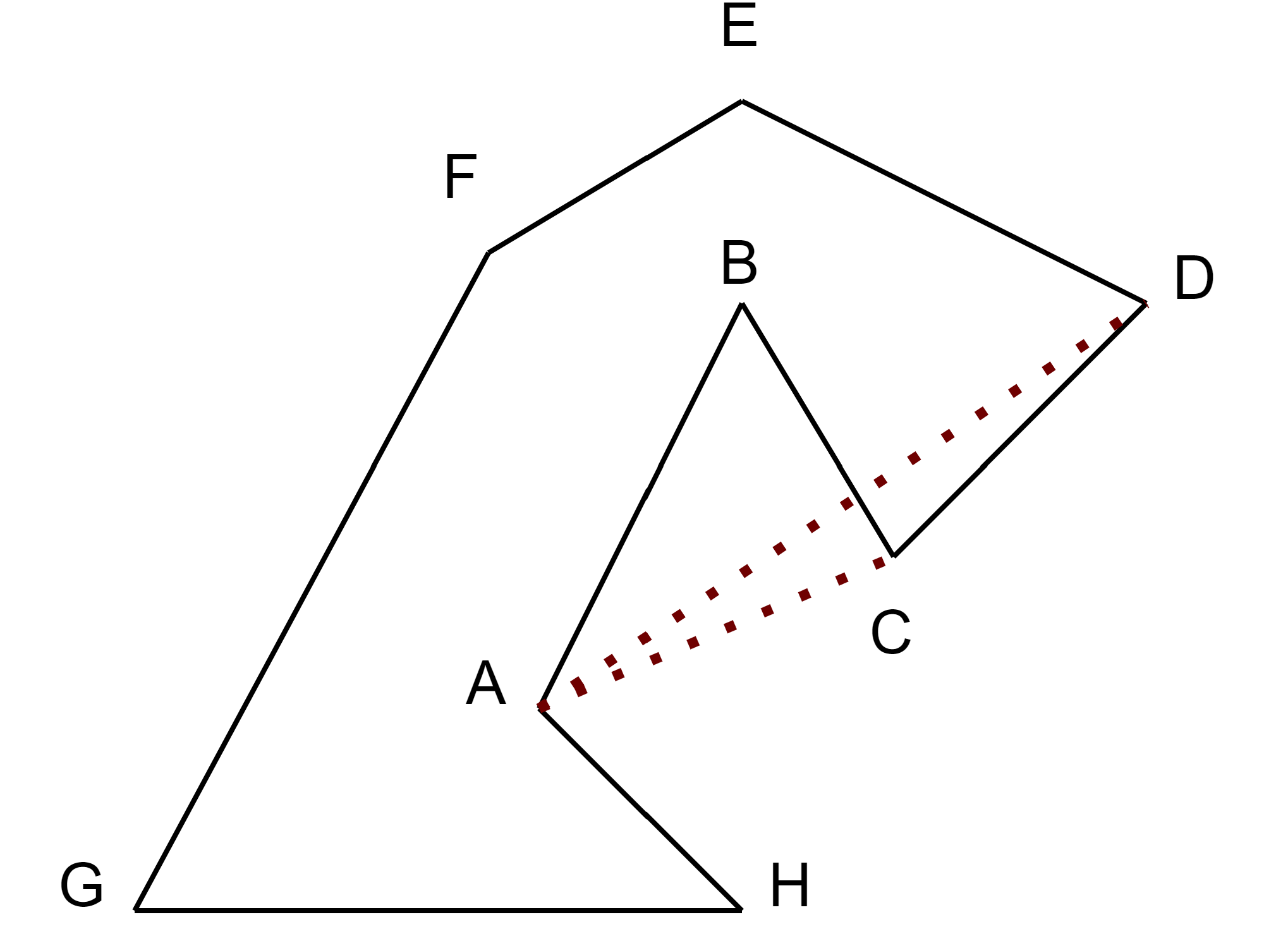
关于在角的内侧，可以看这张图：

线段在角的内侧

图中对角线$AC$位于$∠HAB$和$∠BCD$外侧，而对角线$AD$位于$∠HAB$外侧和$∠CDE$内侧。

对于这个算法来说，其难点就在于：1. 如何找到一个凹的点，2. 如何找到一个完全在内部的对角线。

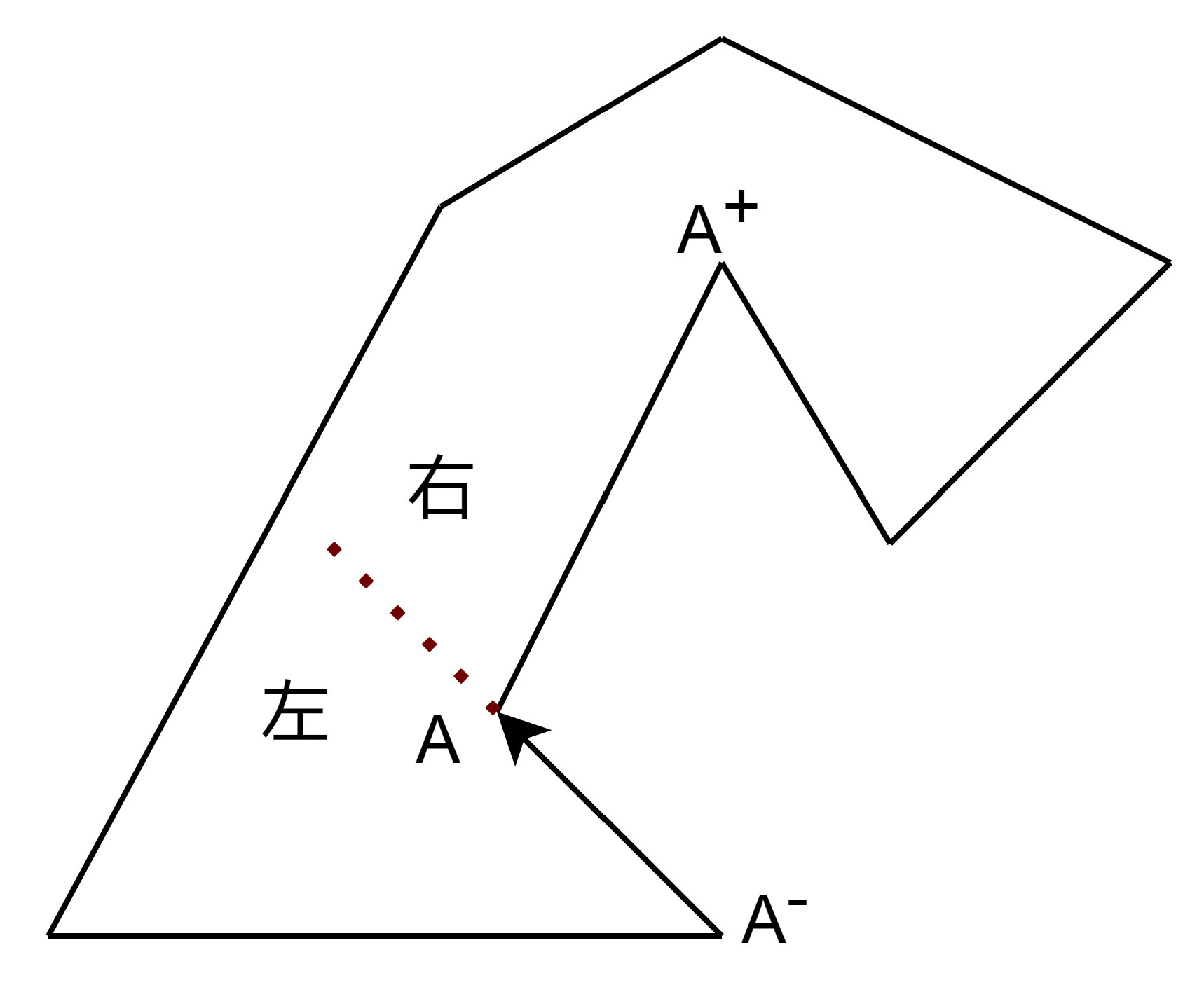
1. 如何找到一个凹的点

我们按照逆时针顺序枚举多边形$P$上的顶点，如下图。当我们枚举到点A时，记录其上一个节点为$A^-$，其下一个节点为$A^+$。通过判断$A^+$与 $\boldsymbol{A^-A}$ 的关系，当$A^+$在$\boldsymbol{A^-A}$的右侧时，则说明点$A$是一个凹的点。

凹的点

我们可以通过向量的叉积来进行左右方向的判断，设$\boldsymbol{A^-A} = (x_1, y_1), \boldsymbol{A^-A^+} = (x_2, y_2)$ 则$\boldsymbol{A^-A} \times \boldsymbol{A^-A^+} = x_1y_2 - x_2y_1$ 。这是一个在$z$轴上的向量，即$(0, 0, x_1y_2-x_2y_1)$。当$A^+$位于$\boldsymbol{A^-A}$左侧时，$x_1y_2-x_2y_1>0$，否则$x_1y_2-x_2y_1<0$，当$A^+$于$\boldsymbol{A^-A}$共线时，$x_1y_2-x_2y_1=0$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/// <summary>
/// 判断点c与向量ab的位置关系
/// </summary>
/// <returns>c在ab左侧，返回1；c在ab右侧，返回-1；c与ab共线，返回0。</returns>
private static int AreaSign(Vector2 a, Vector2 b, Vector2 c)
{
	Vector2 ab = b - a;
	Vector2 ac = c - a;
	
	float area = ab.Cross(ac);

	if (area > EPS) return 1; // c 在 ab 左侧
	else if (area < -EPS) return -1; // c 在 ab 右侧
	else return 0; //a, b, c共线
}

/// <summary>
/// 叉积
/// </summary>
/// <returns>二维向量叉积的模</returns>
public static float Cross(this Vector2 a, Vector2 b)
{
	return a.x * b.y - a.y * b.x;
}

/// <summary>
/// 用于判断点<paramref name="c"/> 是否位于向量ab的左侧。
/// </summary>
/// <returns><paramref name="c"/>位于向量ab左侧为true，否则为false</returns>
public static bool Left(Vector2 a, Vector2 b, Vector2 c)
{
	return AreaSign(a, b, c) > 0;
}

/// <summary>
/// 用于判断点<paramref name="c"/> 是否位于向量ab的左侧或在ab上。
/// </summary>
/// <returns><paramref name="c"/>位于向量ab左侧或在ab上为true，否则为false</returns>
public static bool LeftOn(Vector2 a, Vector2 b, Vector2 c)
{
	return AreaSign(a, b, c) >= 0;
}

/// <summary>
/// 判断点<paramref name="a"/>, <paramref name="b"/>, <paramref name="c"/>是否共线
/// </summary>
/// <returns>三点共线则返回true，否则false</returns>
public static bool Collinear(Vector2 a, Vector2 b, Vector2 c)
{
	return AreaSign(a, b, c) == 0;
}

2. 如何找到一个完全在内部的对角线

对于一个凹的顶点$A$，我们要逐个枚举多边形$P$中不与$A$相邻的其他顶点，然后判断其连线是否是1. 在角的内侧，2. 不与任何非相邻的边相交。

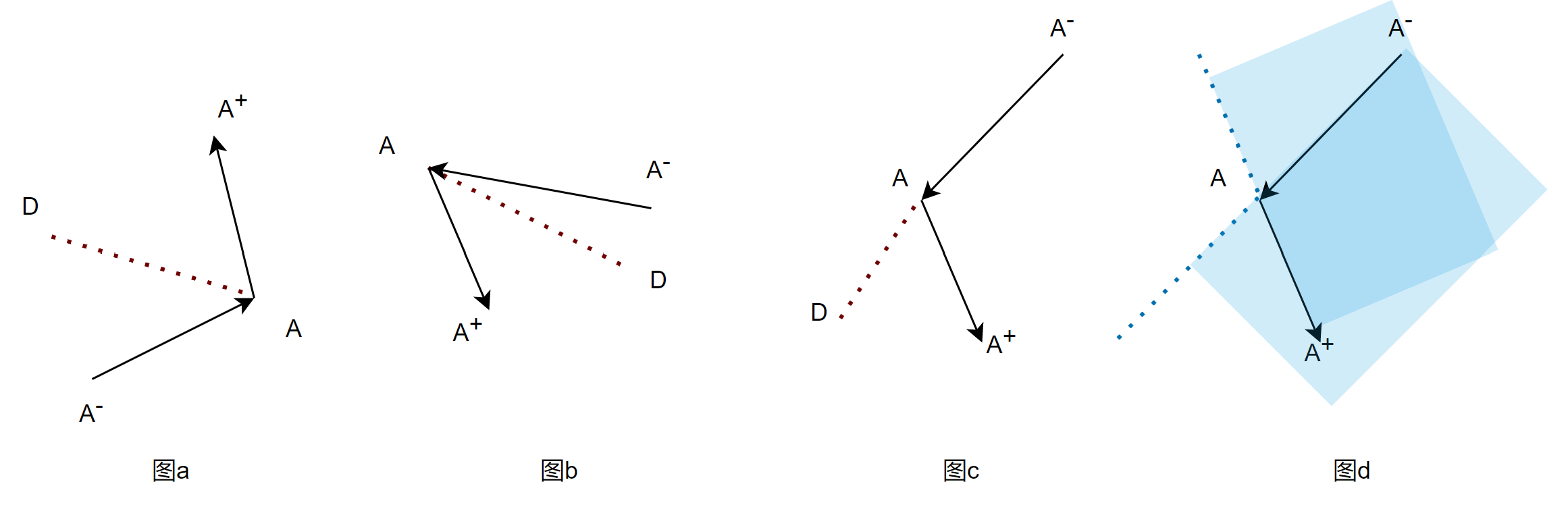
判断是否在角的内侧

如下图a、图b，当$∠A^-AA^+$是个劣角（即小于180°的角）时，要判断$AD$是否在角内部，仅需保证$D$同时在$\boldsymbol{A^-A}$和$\boldsymbol{AA^+}$的左侧。（这里一定要注意我们$A^-,A,A^+$是逆时针排列的）

对于图c，$AD$在$\boldsymbol{A^-A}$的左侧，但是在$\boldsymbol{AA^+}$的右侧，故而其在角的外侧。

在图d中，我们可以看到两个浅蓝色框分别代表$\boldsymbol{A^-A}$和$\boldsymbol{AA^+}$的左侧，则重叠的深色区域就是勇仕在两个向量的左侧的区域，即角的内侧。

判断是否在角的内侧

那当$∠A^-AA^+$为优角（即大于180°小于360°的角）呢？其实可以反向思考以下，这个时候如果$AD$在$∠A^-AA^+$对应的劣角中，岂不就说明$AD$在优角$∠A^-AA^+$外侧了？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/// <summary>
/// 对角线ab是否在∠A内部
/// </summary>
/// <returns>ab在∠A内部返回true，否则false</returns>
public static bool InCone(Vertex a, Vertex b)
{
	Vertex a0 = a.Prev, a1 = a.Next;
	
	// 若∠A为劣角(<180°)
	if (LeftOn(a0.Position, a.Position, a1.Position))
	{
		return Left(a.Position, b.Position, a0.Position)
				&& Left(b.Position, a.Position, a1.Position);
	}

	return !(LeftOn(a.Position, b.Position, a1.Position)
			&& LeftOn(b.Position, a.Position, a0.Position));
}

在上述代码中，引入了一个新类型Vertex，其定义如下：

1
2
3
4
5
6
public class Vertex
{
	public Vector2 Position;
	public Vertex Prev;
	public Vertex Next;
}

目的是将多边形$P$的所有顶点，逆时针方向连接起来。

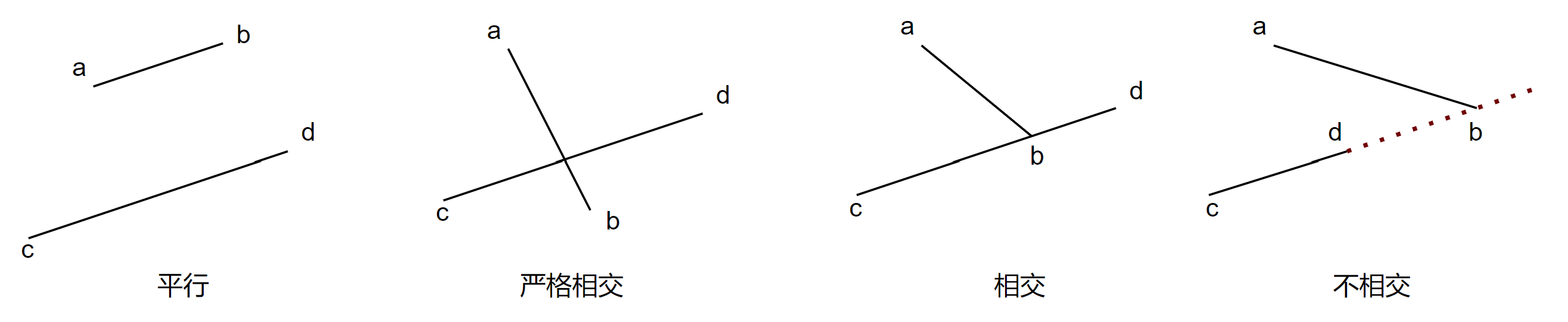
判断是否与其他边相交

我们先来看一下两个线段的位置关系都有哪些，如下图：

两个线段的位置关系

对于严格相交这种情况，我们只需要确保$a, b$在线段$cd$的两侧，并且$c, d$在线段$ab$的两侧即可。如何判断两侧？这就又回到刚才我们判断点在向量左右那一步了，我们可以直接调用刚才写好的Left方法。

对比相交和不相交这两种情况，其区别是三点共线时，共线的点是不是在线段上，即当$bcd$三点共线时，要保证$b$ 位于$cd$之中，就也属于相交的情况。而三点共线也可以直接用刚才写好的Collinear()方法，我们需要再写一个Between()方法去判断当Collinear()满足时，是否满足$b$ 位于$cd$之中这种情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/// <summary>
/// 线段ab与线段cd严格相交
/// </summary>
/// <remarks>严格相交: 不包含三点共线的情况，例如 T 形</remarks>
/// <returns>ab与cd相交，返回true，否则false</returns>
public static bool IntersectStrictly(Vector2 a, Vector2 b, Vector2 c, Vector2 d)
{
	if (Collinear(a, b, c) || Collinear(a, b, d)
		|| Collinear(c, d, a) || Collinear(c, d, b))
		return false;

	return (Left(a, b, c) ^ Left(a, b, d))
			&& (Left(c, d, a) ^ Left(c, d, b));
}

/// <summary>
/// 线段ab与线段cd相交
/// </summary>
/// <returns>ab与cd相交则返回true，否则false</returns>
public static bool Intersect(Vector2 a, Vector2 b, Vector2 c, Vector2 d)
{
	if (IntersectStrictly(a, b, c, d))
		return true;

	if (Between(a, b, c) || Between(a, b, d)
		|| Between(c, d, a) || Between(c, d, b))
		return true;

	return false;
}

/// <summary>
/// 判断在abc共线时，<paramref name="c"/> 是否在 <paramref name="a"/>, <paramref name="b"/> 中间
/// </summary>
/// <returns><paramref name="c"/>在<paramref name="a"/>, <paramref name="b"/>中间则返回true，否则返回false，abc不共线直接返回false</returns>
public static bool Between(Vector2 a, Vector2 b, Vector2 c)
{
	if (!Collinear(a, b, c)) return false;

	if (a.x == b.x)
		return (a.y <= c.y && c.y <= b.y)
				|| (b.y <= c.y && c.y <= a.y);
	else
		return (a.x <= c.x && c.x <= b.x)
				|| (b.x <= c.x && c.x <= a.x);
}

解决了这两个问题后，我们可以用以下代码，解决问题：[[#2. 如何找到一个完全在内部的对角线]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/// <summary>
/// 对角线ab是否与非点 <paramref name="a"/>, <paramref name="b"/> 相邻的边相交
/// </summary>
/// <returns>有相交返回true，否则false</returns>
public static bool DiagonalWithoutIntersect(Vertex a, Vertex b)
{
	Vertex current = a.Next;
	while (current.Next != a)
	{
		Vertex next = current.Next;

		if (current != a && current != b
			&& next != a && next != b
			&& Intersect(current.Position, next.Position, a.Position, b.Position))
			return false;

		current = next;
	}
	
	return true;
}

/// <summary>
/// 对角线ab是否为内部对角线
/// </summary>
/// <remarks>内部对角线: 指对角线完全在多边形的内部</remarks>
/// <returns>ab为内部对角线返回true，否则false</returns>
public static bool Diagonal(Vertex a, Vertex b)
{
	return InCone(a, b) && InCone(b, a) && DiagonalWithoutIntersect(a, b);
}

递归求解

由于我们的Vertex类型中记录了点的前驱Prev和后继Next，所以其实我们只需要拿到多边形中的任意一个点，就可以不断地通过Next获取到多边形中所有的顶点。所以我们可以定义如下多边形polygon类型：

1
2
3
4
5
6
7
8
public class Polygon
{
	public Vertex StartVertex => _startVertex;
	
	private Vertex _startVertex;

	#region Methods...
}

然后定义方法Split()去不断的完成本文最开头的5条方法步骤。不过在这里还有几个细节要处理。

分割过程

可以看到，在以$AC$为对角线，分割$P$为$P1,P2$后，需要补充两个点$A^\prime,C^\prime$。这一部分主要是各种链表的操作（因为我们用Prev,Next等将Vertex连接起来，其实就是一个双向循环链表）。在如下代码中，我标注了每个变量对应上图中的点，方便对照看去理解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
/// <summary>
/// 将Polygon分割成若干凸多边形，使用 divide-and-conquer 方法；
/// 该方法基于 Arkin, Ronald C.的论文
/// "Path planning for a vision-based autonomous robot".
/// </summary>
/// <returns>凸多边形数组，即此多边形的分割结果。</returns>
public List<Convex> Split()
{
	List<Convex> convexList = new List<Convex>();
	
	// 寻找一个凹的顶点 concave 对应上图的C点
	Vertex concave = FindConcaveVertex();

	if (concave == null)
	{
		// 没找到凹的顶点，说明this本身就是凸多边形
		convexList.Add(new Convex(this));
		return convexList;
	}
	else
	{
		// 找一个poly上的点，和concave组一个内部对角线，将poly分割成两部分
		Vertex splitVertex = null;
		Vertex current = _startVertex;
		do
		{
			if (BasicOperations.Diagonal(current, concave))
			{
				splitVertex = current;
				break;
			}
			current = current.Next;
		} while (current != _startVertex);

		// 这种情况理论上不会发生 //TODO: 报个Warning
		if (splitVertex == null) { return null; }
		// splitVertex对应上图中的A点
		
		// 将此多边形拆分成两个子多边形
		Vertex splitVertexNext = splitVertex.Next; // 对应上图B点
		Vertex concavePrev = concave.Prev; // 对应上图B点

		// 将AC连接起来
		splitVertex.Next = concave;
		concave.Prev = splitVertex;

		// A点的补充点 A'
		Vertex suppliedSplitVertex = new Vertex(splitVertex.Position);
		// C点的补充点 C'
		Vertex suppliedConcave = new Vertex(concave.Position);

		// 将A'C'连接起来
		suppliedSplitVertex.Prev = suppliedConcave;
		suppliedConcave.Next = suppliedSplitVertex;

		// 将A'和B连接起来，C'和B连接起来
		suppliedSplitVertex.Next = splitVertexNext;
		splitVertexNext.Prev = suppliedSplitVertex;
		suppliedConcave.Prev = concavePrev;
		concavePrev.Next = suppliedConcave;

		// 生成P1，P2
		Polygon childPolygon1 = new Polygon(concave);
		Polygon childPolygon2 = new Polygon(suppliedConcave);

		// 递归求解
		convexList.AddRange(childPolygon1.Split());
		convexList.AddRange(childPolygon2.Split());
	}

	return convexList;
}

这里我们引入了一个新类型Convex表示凸多边形。当然我们可以让Convex类继承自polygon，不过我们并不需要Convex包含太多方法（例如Split()等），故而我们单独开一个类表示它。

1
2
3
4
5
6
public class Convex
{
	public Vertex StartVertex => _startVertex;

	private Vertex _startVertex;
}

孔洞的处理

到此为止其实我们已经可以很好的将一个任意多边形分割成若干凸多边形了，但是我们忽略了一个很重要的事，就是中间有孔的多边形应该怎么处理？

对于孔洞的处理算法，来源于 Recast Navigation

首先孔也是一个多边形，我们记为$Hole$ 。

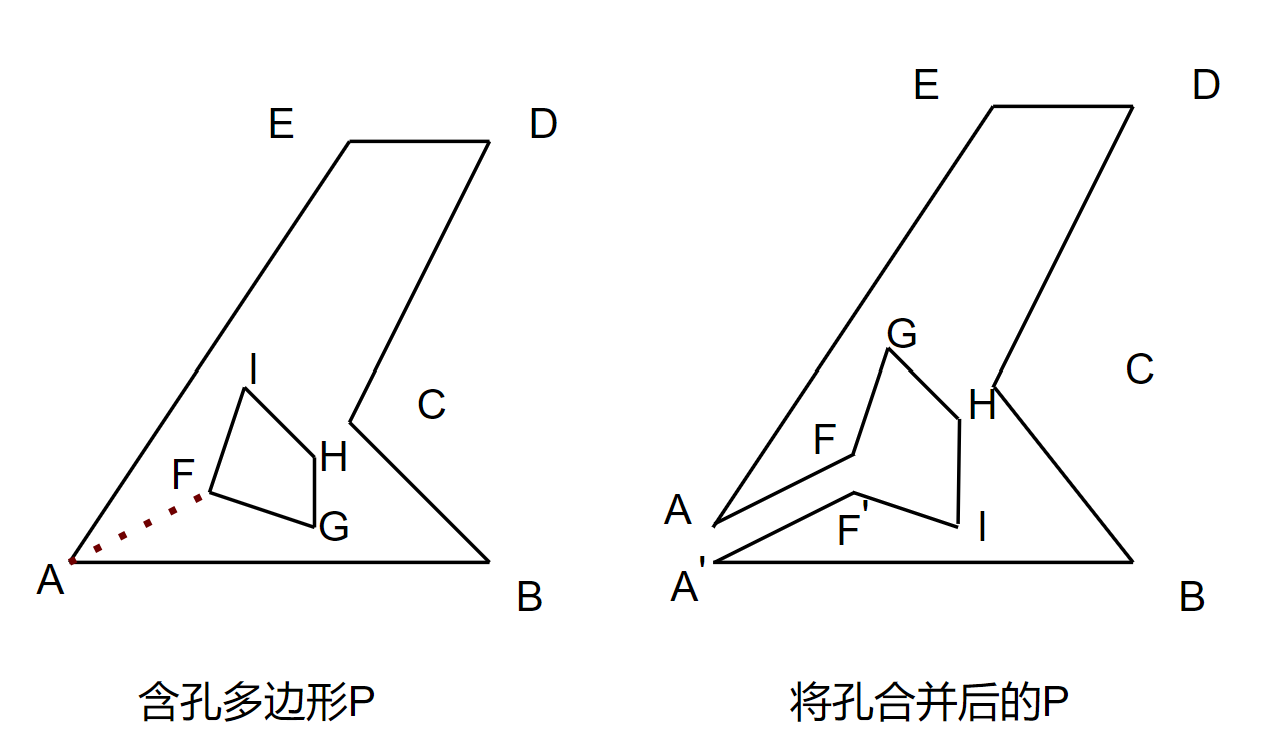
  1. 在$Hole$中选择一个顶点（如下图$F$）

  2. 在$P$上选择一个顶点（如下图$A$），且$AF$不与$P$或$Hole$上的任意非$A, F$相邻边相交

孔洞的处理

不合法的选择，例如$FC$，会与$Hole$上的边$IH$相交；例如$GD$，会与$P$上的边$BC$相交。

  1. 沿着选择的连线（如上图$AF$），将$P$与$Hole$融合

这里要时刻记住我们的多边形，顶点都是按照逆时针顺序连接的，$Hole$也不例外。然而当我们融合时，需要顺时针将$Hole$上的顶点添加到$P$中，这样得到的$P$的顶点才满足逆时针连接的条件。所以这里我们需要经过一个类似反转链表的过程。当然和之前相同的，这里我们也需要补充两个点$A^\prime,F^\prime$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/// <summary>
/// 处理中间包含孔的多边形
/// </summary>
public void MergeHole(Polygon hole)
{
	if (!HasInnerPolygon(hole)) // hole必须在多边形内部才有必要去合并
		return; 

	bool hasFound = false;
	Vertex linkVertPoly = null, linkVertHole = null;
	Vertex holeVertex = hole.StartVertex;
	
	// 在P和hole上找到两个点，用其连线合并P和hole 
	do
	{
		Vertex vert = StartVertex;
		do
		{
			// vert - holeVertex 线段，不与P或者hole上的任何一个非相邻边相交
			if (BasicOperations.DiagonalWithoutIntersect(vert, holeVertex)
				&& BasicOperations.DiagonalWithoutIntersect(holeVertex, vert))
			{
				linkVertPoly = vert; // 对应上图中的点A
				linkVertHole = holeVertex; // 对应上图中的点F
				hasFound = true;
				break;
			}
			vert = vert.Next;
		} while (vert != StartVertex);

		if (hasFound) break;
		holeVertex = holeVertex.Next;
	} while (holeVertex != hole.StartVertex);

	// 将P与hole融合
	if (hasFound)
	{
		// 将A和F连接起来
		Vertex linkVertPolyNext = linkVertPoly.Next; // 对应上图点B
		linkVertPoly.Next = linkVertHole;
		Vertex linkVertHolePrev = linkVertHole.Prev; // 对应上图点I
		linkVertHole.Prev = linkVertPoly;

		// 反转链表
		// 在上图中可以看到F->I->H->G变成了F->G->H->I
		// 但是在实现的时候，并不会更换顶点，而是将Next指针和Prev指针做个交换
		Vertex prev = linkVertHole, current = linkVertHolePrev;
		while (current != linkVertHole)
		{
			Vertex currentPrev = current.Prev;
			prev.Next = current;
			current.Prev = prev;

			prev = current;
			current = currentPrev;
		}

		// 补充linkVertHole重合节点， 对应上图的点F'
		var suppliedLinkVertHole = new Vertex();
		suppliedLinkVertHole.Position = linkVertHole.Position;
		// 连接I和F'
		suppliedLinkVertHole.Prev = prev;
		prev.Next = suppliedLinkVertHole; 

		// 补充linkVertPoly重合节点， 对应上图的点A'
		var suppliedLinkVertPoly = new Vertex();
		suppliedLinkVertPoly.Position = linkVertPoly.Position;
		// 连接A'F'
		suppliedLinkVertPoly.Prev = suppliedLinkVertHole;
		suppliedLinkVertHole.Next = suppliedLinkVertPoly;
		// 连接A'B
		suppliedLinkVertPoly.Next = linkVertPolyNext;
		linkVertPolyNext.Prev = suppliedLinkVertPoly;
	}
}

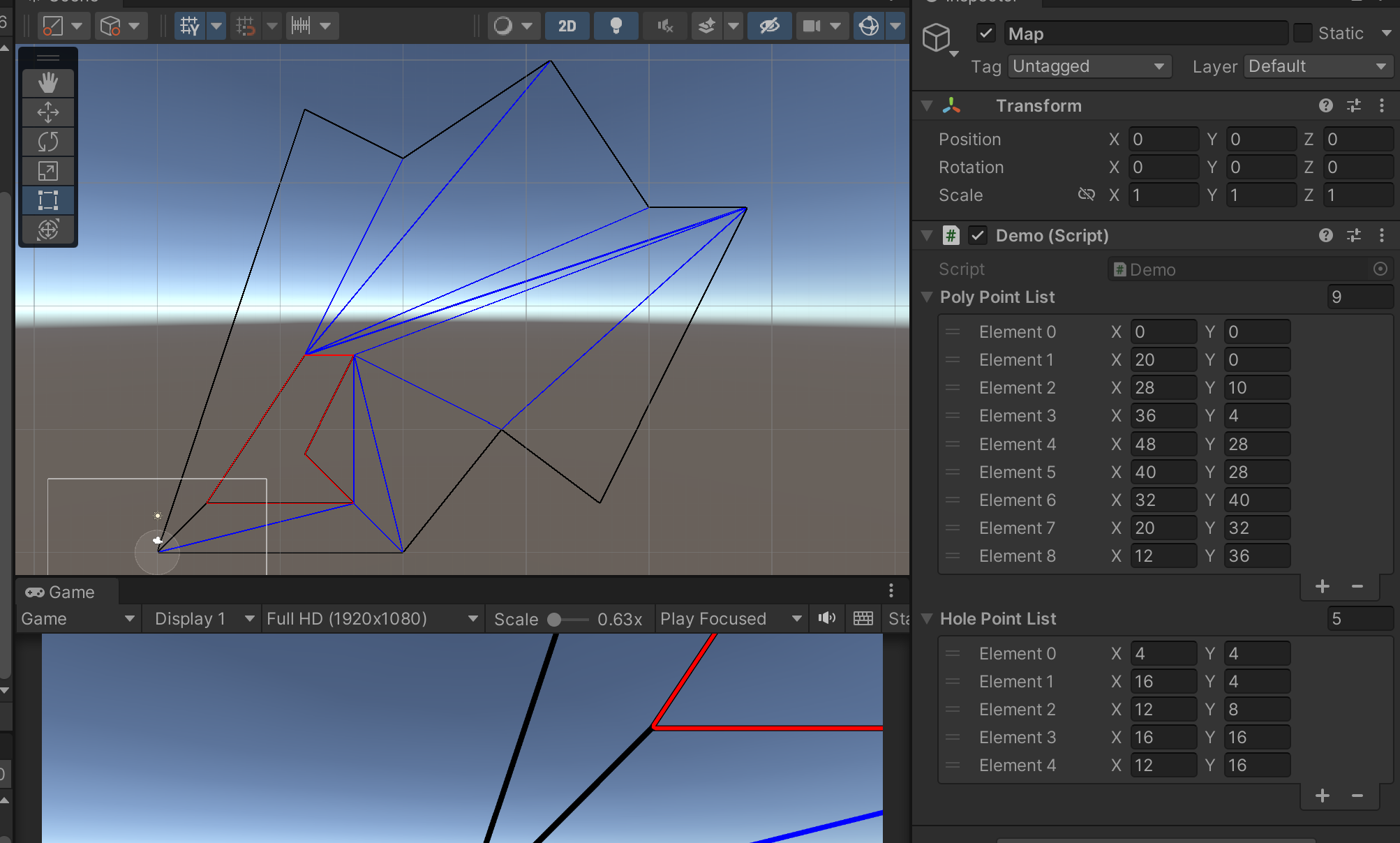
在Unity中展示

当我们完成了全部的计算任务后，就可以在Unity中，将多边形绘制出来了。在这里我利用Unity自带的lineRenderer进行线段的绘制。

演示效果

再上图中，可以在Inspector窗口编辑多边形$P$以及孔洞$Hole$的个顶点坐标（注意要按照逆时针顺序），用黑色的线绘制出了$P$，用红色的线绘制出了$Hole$，蓝色的线即分割线。注意有一条黑色的线连接了$P$和$Hole$，这即是我们选择来融合$P$和$Hole$的连接线

补充知识

判断一个多边形是否在另一个多边形内部

在MergeHole()方法中有一段代码：

1
2
if (!HasInnerPolygon(hole)) // hole必须在多边形内部才有必要去合并
	return;

进行了两个多边形相容性的判断，当$hole$完全被$P$包含时，返回true，并进行后续的融合操作。

而这里如何判断一个多边形是否被另一个多边形包含，是通过判断$hole$中的每个顶点是否在$P$中，若$hole$的全部顶点都在$P$中，则认为$hole$被$P$包含。由此将问题转化为了：如何判断一个顶点是否在一个多边形中。

解决这个问题有一个很经典的方法：

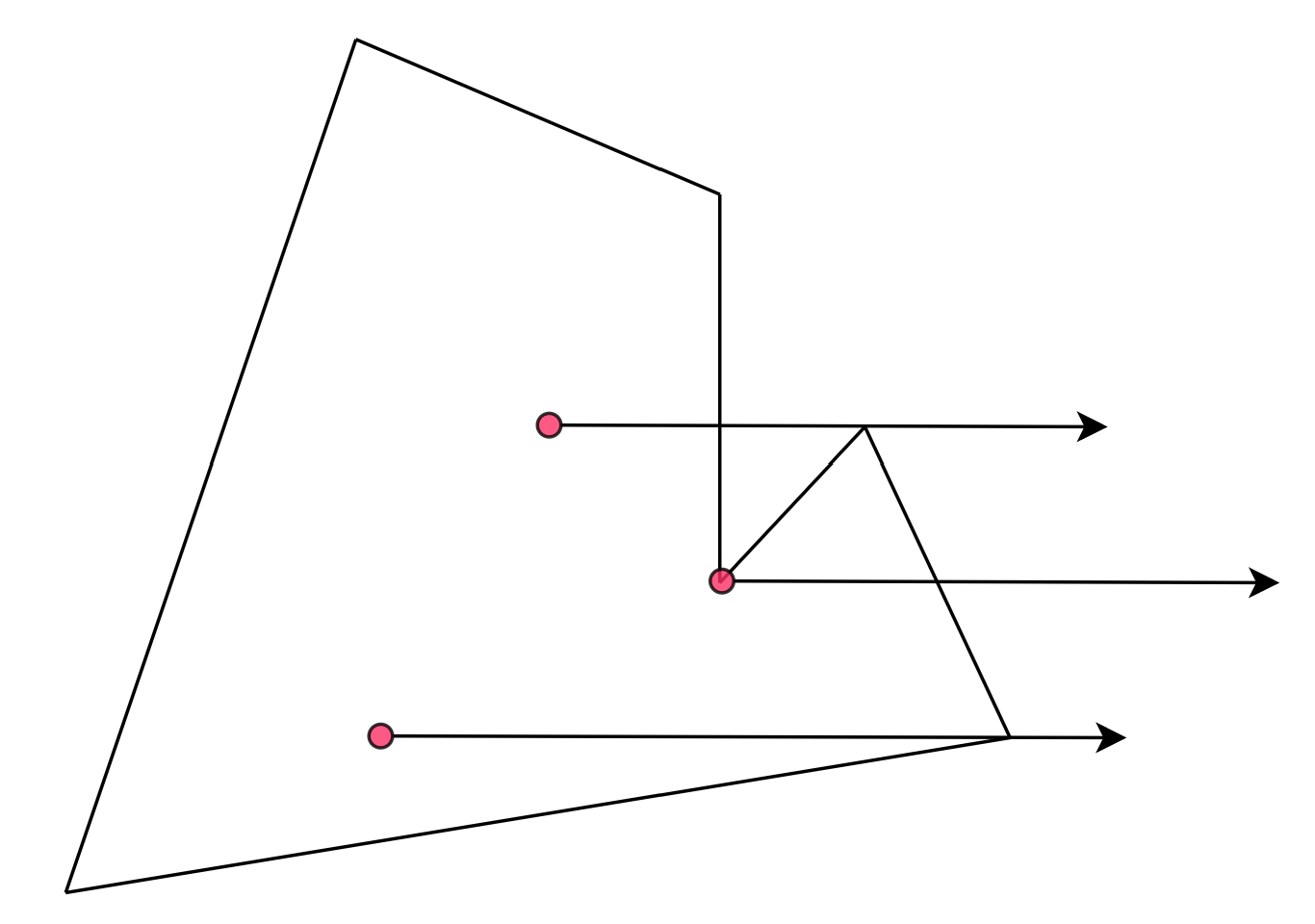
引射线法： 从目标点出发引一条射线（我们可以取水平向右的射线），看这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。

看上去很好实现，只需要$O(n)$枚举多边形的每条边，然后判断是否相交即可，但是其实还是有不少细节的。

例如下图中这种过顶点的情况，如果不确定好统计规则，很容易顶点两条边都被记录一次，导致本在内部被判定为在外部（例如最下方的红点，经过多边形的顶点，会被记为经过了两条边）

引射线法

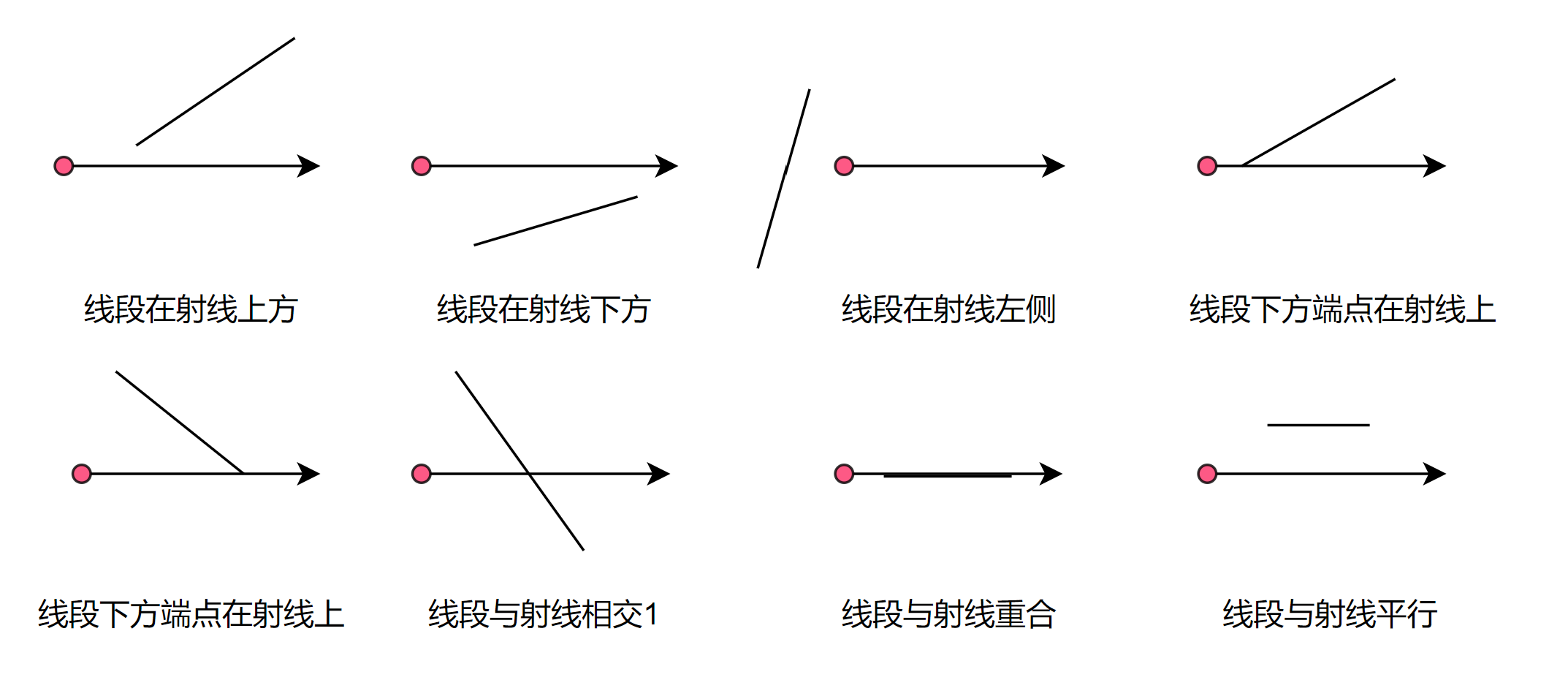
此外，线段与射线的关系可以用下图展示：

线段与射线的关系

我们可以很容易的判断线段在射线的上、下、左、重合/平行。为了处理前面说的过顶点的情况，我们认为经过线段下侧端点的射线与线段不相交。而剩下的就是计算一下线段上对应射线所在$y$坐标点的$x$坐标值，和射线起点的$x$坐标值作比较，如果大于射线起点的$x$坐标，则说明有交点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/// <summary>
/// 从 <paramref name="raySource"/>发出的水平向右的射线，是否与线段ab相交
/// </summary>
/// <returns>相交则返回true，否则返回false</returns>
public static bool HorizontalRayIntersectSegment(Vector2 raySource, Vector2 a, Vector2 b)
{
	if (a.y == b.y) return false;                               // 线段与射线平行、重合
	if (a.y > raySource.y && b.y > raySource.y) return false;   // 线段在射线上方
	if (a.y < raySource.y && b.y < raySource.y) return false;   // 线段在射线下方
	if ((b.y < a.y && b.y == raySource.y)
		|| (a.y < b.y && a.y == raySource.y)) return false;     // 射线与下方端点相交
	if (a.x < raySource.x && b.x < raySource.x) return false;   // 线段在射线左边

	var x = b.x - (b.x - a.x) * (b.y - raySource.y) / (b.y - a.y); // 求交点x坐标
	return x >= raySource.x;
}

补充阅读

留白- Recast Navigation 源码剖析 01 - Meadow Map论文解析与实验

文章作者: FcAYH
文章链接: http://www.fcayh.cn/2022/11/28/meadow-map/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Forever丶CIL！
C#Unity计算几何NavMesh